Topic Overview
Research and development organization
Research and Development Project Leader
Koji Terashi (Associate Professor at the International Center for Elementary Particle Physics, the University of Tokyo.)
Participating institutions (Educational)
The University of Tokyo / Keio University / RIKEN (Rikagaku Kenkyūsho) / Okinawa Institute of Science and Technology Graduate University / The University of Chicago
Participating institutions (Corporate)
SCSK Corporation / NS Solutions Corporation / International Business Machines Corporation / blueqat Corporation / Mitsubishi UFJ Financial Group, Inc.
Characteristics of this topic
- Performance demonstration of quantum machine learning with realistic data in the regime of small amounts of data and a limited number of parameters.
- Examples include image recognition using quantum reservoir methods, classification of particle physics data, and data classification using quantum GANs.
- Quantum machine learning with quantum data as input will establish an advantage over classical machine learning.
- Models that enable learning and inference with different quantum devices enhance versatility.
- Acceleration of societal implementation.
Objective of this topic
- Quantum computer model proposal for efficient implementation of high generalization quantum machine learning models.
- Performance evaluation through applications in particle physics experiments and quantum simulations of many-body problems.
- Development of quantum machine learning models with data from quantum embedding.
- Quantitative evaluation of performance and verification of advantages on quantum computers with 50 or more qubits.
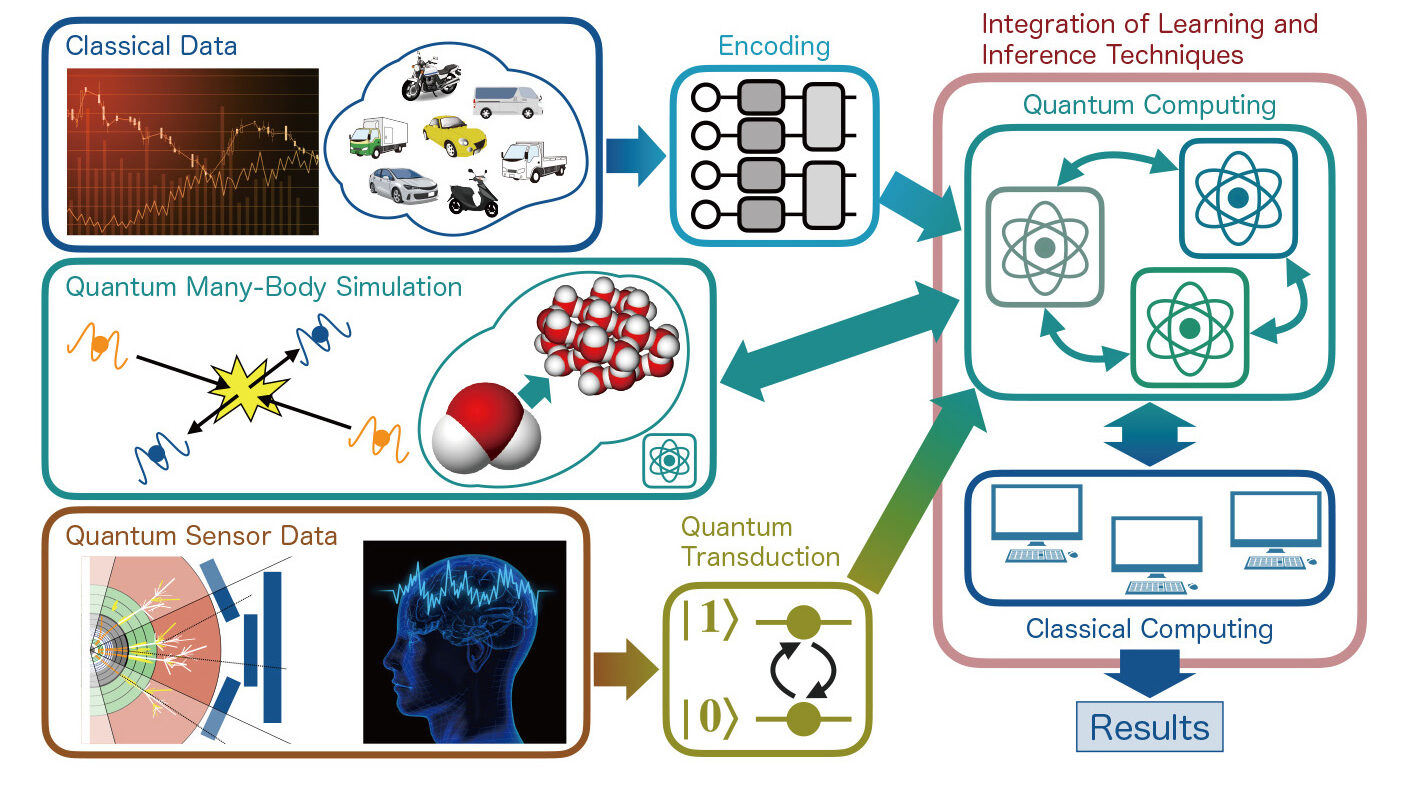
Research Highlights
Avoiding the vanishing gradient problem
- For quantum machine learning with classical data as input, the problem of vanishing gradients can occur.
- Necessary conditions to avoid gradient vanishing have been sought.
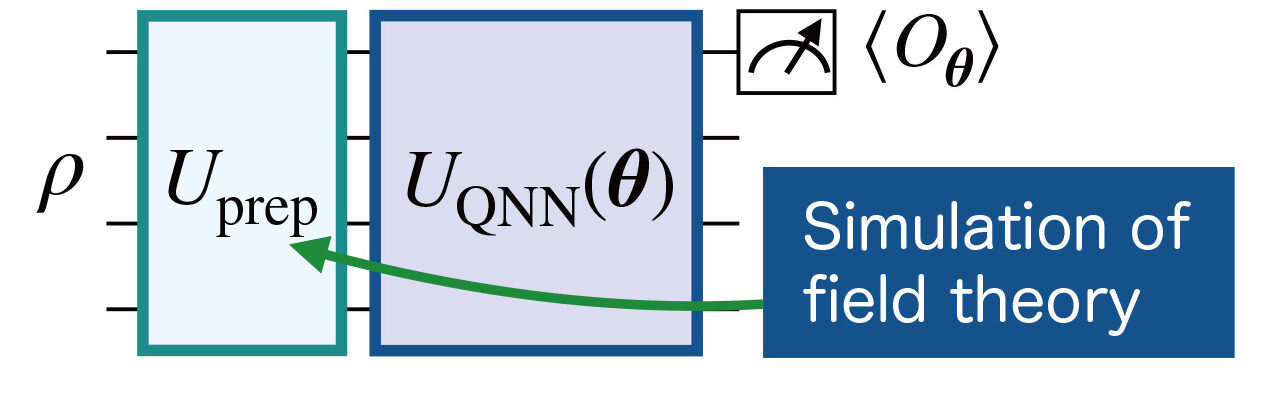
- In quantum machine learning with quantum data as input, learning models have been implemented to directly input the wave function of physical systems and predict their physical properties.
- This approach represents the first attempt to apply quantum machine learning to quantum data from the simulation of quantum field theory. It has been confirmed that learning is possible even for non-trivial states, such as those from real-time dynamics and multi-particle generation.
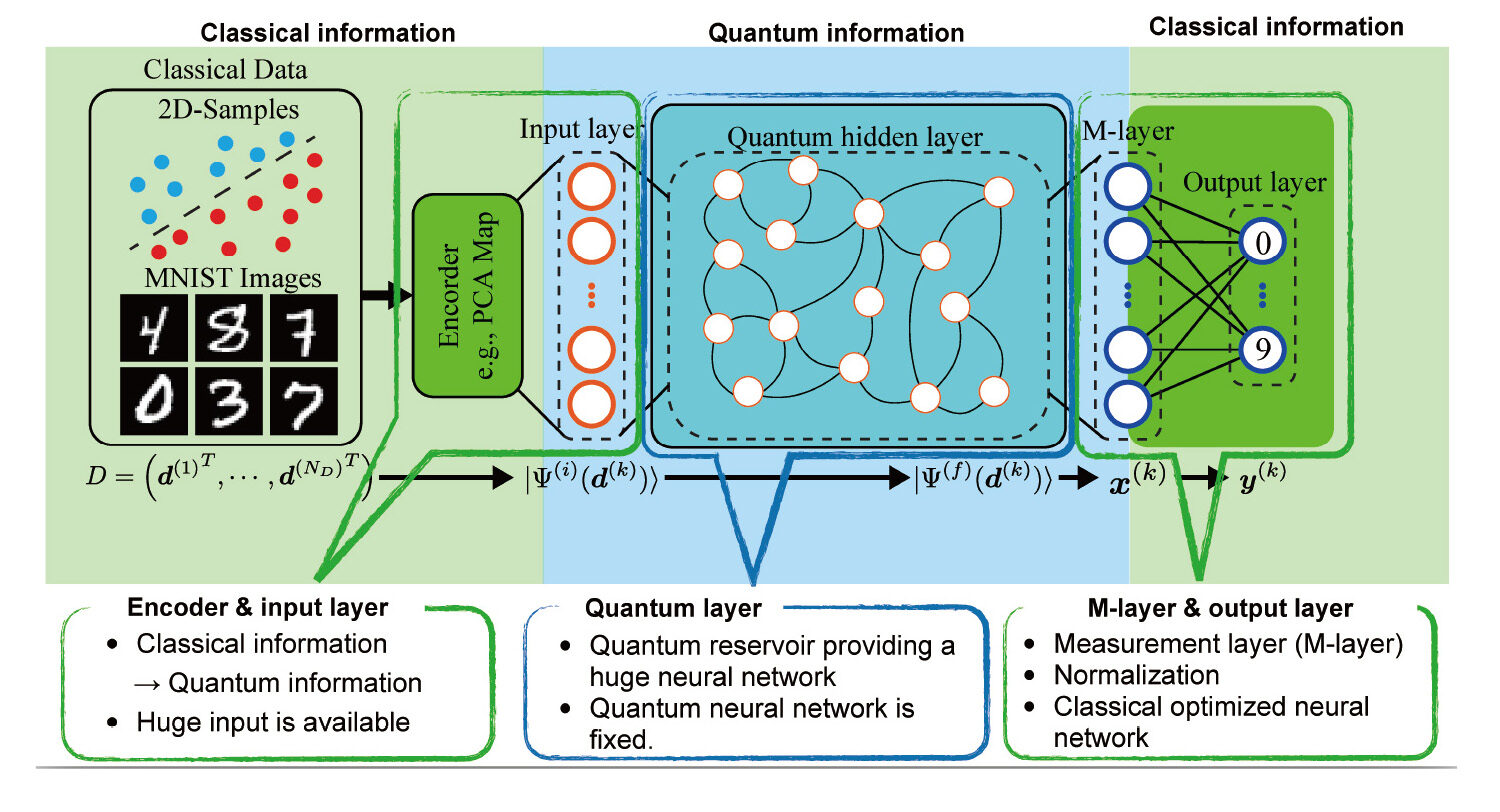
Quantum extreme reservoir computational model
- We generated classification problems in a 2D space, examined the performance of the quantum extreme reservoir model, and verified its stability.
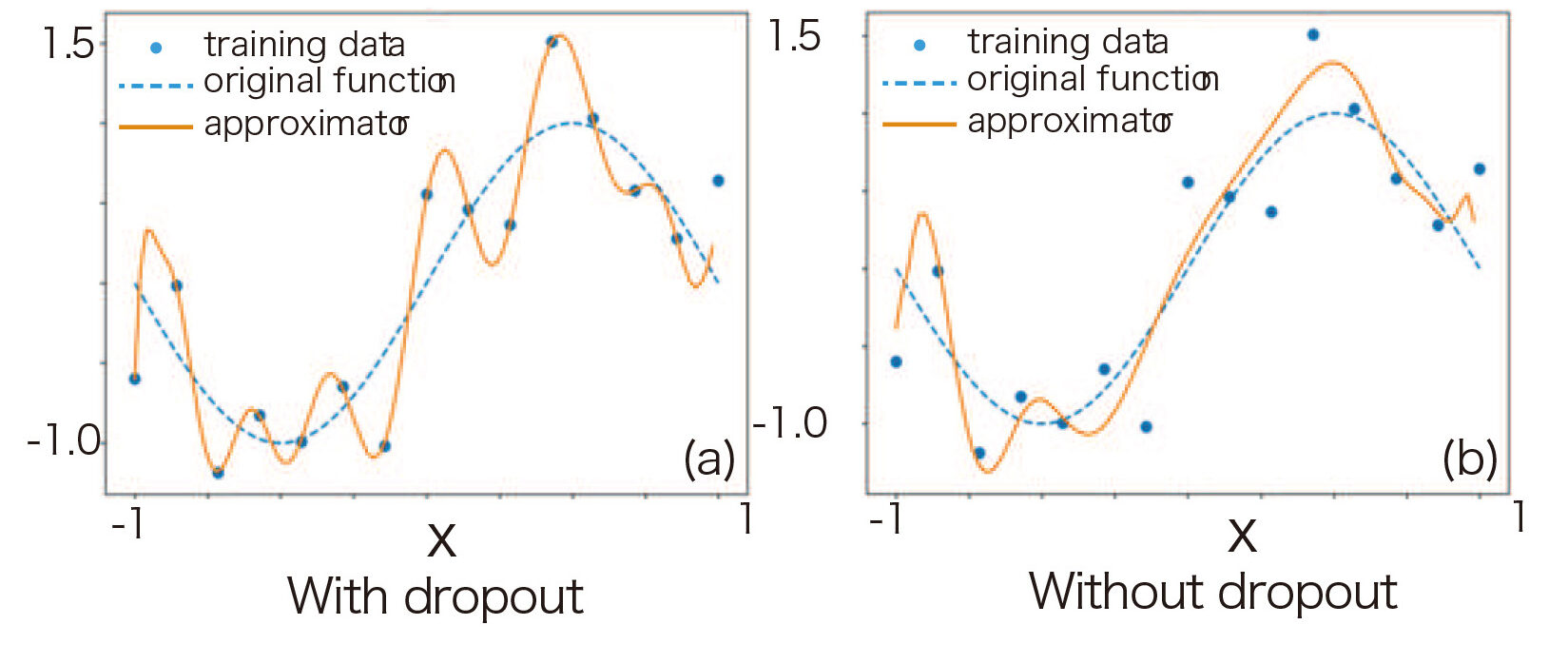
Overfitting in quantum machine learning
- Quantum computers have the potential to perform machine learning more effectively than conventional computers.
- We are developing methods for generating surrogate models with quantum machine learning, including the method of avoiding overfitting due to too-expressive circuits.
- It is possible to reduce the expressibility of quantum circuits by randomly deleting entangling gates and introducing dropouts similar to those in classical systems.
- It has been shown that overfitting can be suppressed by exploiting these dropouts.
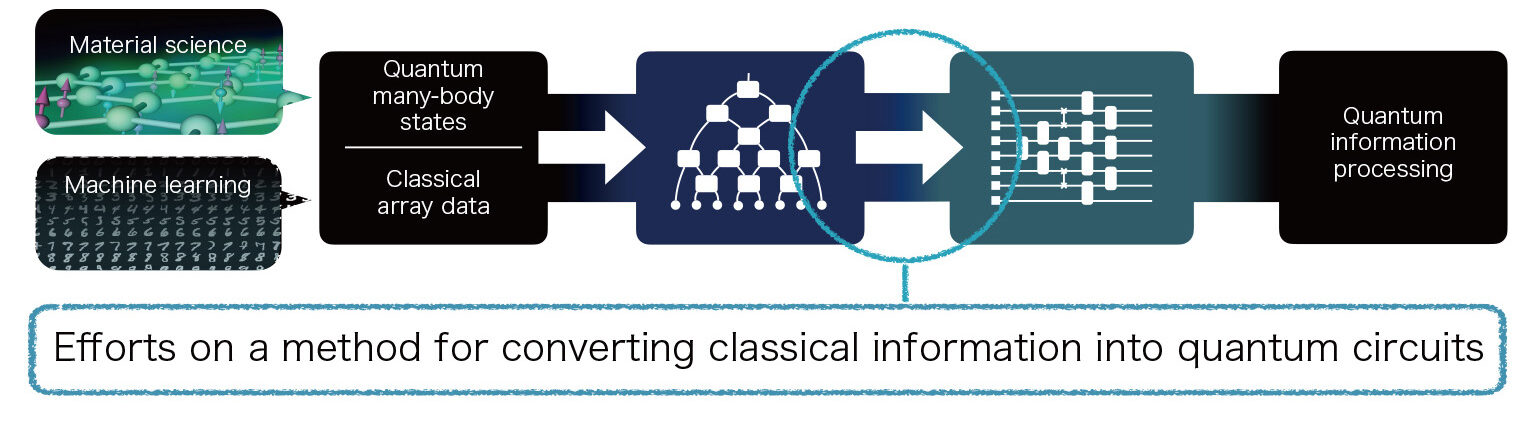
Quantum circuits for classical information
- We propose a quantum-classical hybrid algorithm to encode an arbitrary quantum state in an optimal quantum circuit with a finite number of one- and two-qubit quantum gates.
- Numerical simulations demonstrate the algorithm to encode the ground state of quantum many-body systems, including the spin-1/2 antiferromagnetic Heisenberg model and the spin-1/2 XY model.
- This algorithm allows us to construct an optimal quantum circuit when classical information, such as images, is encoded in quantum states.
- This algorithm can be used for machine learning of classical data on a quantum computer.
Future Prospects
- Understanding the generalization and application scope of quantum machine learning:
- Exploration of new applications in different computational tasks.
- Investigation of robust techniques to mitigate the issue of gradient vanishing, such as introducing symmetries or incorporating overparameterization
- Efficient encoding of classical data into quantum circuits:
- Application of quantum embedding techniques, such as tensor networks, for efficient encoding of classical data in machine learning tasks.
- Evaluation methods for generalization and advantages in quantum data learning:
- Assessing the generalization performance and advantages in quantum data learning.
- Evaluating the performance of quantum generative models for predicting physical properties. Generalization performance with input from quantum field theory simulation and comparison with classical approach (order parameter measurement).
- Interface between quantum simulation/quantum sensing device and quantum computers:
- Preliminary research on quantum state conversion protocols (quantum transduction)/investigating the applications of quantum computers.
